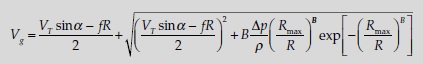Catastrophe Derivatives and ILWs

INDEX-LINKED CONTRACTS

Traditional insurance and reinsurance contracts are based purely on direct
indemnification of the insured or reinsured for the losses suffered. Another
way to transfer insurance risk, which is particularly important in its transfer
to the capital markets, is to link the payments to a certain value of an index
as opposed to basing it only on the reimbursement of the actual losses
suffered by a specific entity.

An example of such an index would be that of
the level of losses suffered from a hurricane in a particular region by the
whole insurance industry. Another example would be a purely parametric
one based on the intensity of a specified catastrophic event without referencing
actual insured losses.

The two main types of insurance-linked securities whose payout depends
on an index value are insurance derivatives and industry loss warranties.
Industry loss warranties (ILWs) and catastrophe derivatives (a subset of
insurance derivatives) were the first insurance-linked securities to appear.
ILWs were first introduced in the 1980s and at the time they were often
referred to as original loss warranties (OLWs) or original market loss
warranties.

The first catastrophe derivative contracts were developed in
1992 by the Chicago Board of Trade (CBOT). Both types of contract have
since evolved; their markets have evolved as well. ILWs in particular are
now playing an important role in the transfer of catastrophe risk from insurance
to capital markets.

The use of an index as a reference offers the transparency and lack of
moral hazard that are so important to investors. The ease of standardisation
is also important. One of the key advantages, not yet fully realised, is the
liquidity and price discovery that come with exchange-traded products such
as catastrophe derivatives.

This article provides an overview of ILWs and catastrophe derivatives
and explains the considerations used in their analysis by investors and
insurers. It then describes the standard indexes used in structuring these
securities and gives some specific examples.

The focus is on property insurance
risk transfer; insurance derivatives linked to mortality and longevity
are explained in the chapters dealing with mortality and longevity risk
trading, while weather derivatives are discussed in Chapter 8. Finally, the
present chapter examines the trends in the market for ILWs and catastrophe
derivatives and the expectations for its growth and evolution.

ROLE OF AN INDEX

Index-linked investments are common in the world of capital markets. The
indexes used in insurance and reinsurance risk analysis are typically related
to the level of insurance losses; these are not investable indexes and neither
are their components. A derivative contract can still be structured based on
such an index, but the underlying of the derivative contract is not a tradable
asset.

In the transfer of insurance risk, an index is chosen in such a way that
there is a direct relationship between the value of the index and the insurance
losses suffered. There is, however, a difference between the two: the
basis risk. This risk is not present when a standard reinsurance mechanism
is utilised.

While index-linked products are used primarily for the transfer of true
catastrophe risk, there is a growing trend of transferring higher-frequency
(and lower-severity) risk to the capital markets. The indexes used do not
necessarily have to track only catastrophic events.

CATASTROPHE DERIVATIVES DEFINED

In financial markets, a derivative is a contract between two parties the value
of which is dependent on the value of another financial instrument known
as an underlying asset (usually referred to simply as an underlying). A
derivative may have more than one underlying. In the broader sense, the
underlying does not have to be an asset or a function of an asset.

Catastrophe derivatives are such contracts, with an underlying being an
index reflecting the severity of catastrophic events or their impact on insurance
losses.

Futures are an example of derivative instruments. Catastrophe futures are
standardised exchange-traded contracts to pay or receive payments at a
specified time, with the value of the payment being a function of the value of an index. Unlike the case of traditional financial futures, physical delivery
of a commodity or other asset never takes place.

Options are another example of financial derivatives; they involve the right to buy (call option)
or sell (put option) an underlying asset at a predetermined price (strike). In
the context of catastrophe derivatives, of particular importance are call
spreads, which are the combination of buying a call at a certain strike price
and selling a call on the same underlying at a higher strike, with the same
expiration date.

The calls can be on catastrophe futures. Using a call spread
limits the amount of potential payout, making the contract somewhat
similar to reinsurance, where each protection layer has its own coverage
limit.

Binary options provide for either a fixed payment at expiration or,
depending on the value of the underlying, no payment at all. In other words,
there are only two possible outcomes. They are also referred to as digital
options.

There are numerous ways that catastrophe derivatives can be structured.
The payout may depend on a hurricane of specific magnitude making a
landfall in a certain area; on the value of total cumulative losses from hurricanes
to the insurance industry over a certain period of time for a specified
geographical region; or on the value of an index tracking the severity of an
earthquake at several locations.

The flexibility in structuring an over-thecounter
(OTC) derivative allows hedgers to minimise their basis risk. At the
same time, there are significant advantages to using standard instruments
that can be traded on an exchange.

Exchange-traded derivatives are more
liquid, allow for quicker and cheaper execution, provide an effective mechanism
for managing credit risk and bring price transparency to the market,
all of which are essential for market growth.

Derivatives versus reinsurance

All insurance and reinsurance contracts may be seen as derivatives, albeit
not recognised as such by accounting rules. Technically, they would be call
spreads, which corresponds to policy limits in insurance. From the point of
view of the party being paid for assuming the risk, an excess-of-loss reinsurance
contract can be seen as being equivalent to selling a call with the
strike at the attachment point and buying a call with the strike equal to the
sum of the attachment point and the policy limit. The “underlying” in this
case is the level of insurance losses.

The true derivatives such as insurance catastrophe derivatives have a
better defined and stable underlying and are accounted for as financial derivative products. Insurance accounting is not allowed for these products.
This topic will be revisited later in the article.

INDUSTRY LOSS WARRANTIES DEFINED

The term “industry loss warranty” (ILW) has been used to describe two
types of contract, one of them a derivative and the other a reinsurance
contract. In its most common form, an ILW is a double-trigger reinsurance
contract. Both trigger levels have to be exceeded for the contract to pay. The
first is the standard indemnity trigger of the reinsured suffering an insured
loss at a certain level, that is, the ultimate net loss (UNL) trigger.

The second is that of industry losses or some other index level being exceeded. The
index of industry losses can be, for example, the one determined by the
Property Claim Services (PCS) unit of Insurance Services Office, Inc. (ISO).
An ILW in a pure derivative form is a derivative contract with the payout
dependent only on the industry-based or some other trigger as opposed to
the actual insurance losses of the hedger purchasing the protection. Even
though labelled an ILW, it is really an OTC derivative such as the products
described above.

The choice between the ILW reinsurance and derivative forms of protection
has significant accounting implications for the hedger. It is typically
beneficial for the hedger to choose a contract that can be accounted for as
reinsurance, with all the associated advantages. This is why the vast
majority of ILW transactions are done in the form of reinsurance.

The majority of ILWs have a binary payout, and the full amount is paid
once the index-based trigger has been activated. (We assume that the UNL
trigger condition, if present, has been met.) However, some ILW contracts
have non-binary, linear payouts that depend on the level of the index above
the triggering level. There seems to be general market growth in all of these
categories.

MARKET SIZE

While the size of the catastrophe bond market is known, it is difficult to estimate
the volume of the industry loss warranty and catastrophe derivative
market. The OTC transactions are rarely disclosed, leading to a wide range
of estimates of market size. The only part of the market with readily available
data is that of exchange-traded catastrophe derivatives. The exchanges
report the open interest on each of their products.

While its size is not very big (with no estimates exceeding US$10 billion
in limits), this market is important as a barometer of reinsurance rates and their movements. Exchange-traded products bring price transparency to the
traditionally secretive reinsurance market. The growing activity of ILW
brokers is leading to increased transparency in the OTC markets as well.
While not directly comparable to traditional reinsurance contracts, catastrophe
derivatives and ILWs provide an important reference point in
pricing reinsurance protection.

It is likely that in terms of total limits, the ILW and catastrophe derivative
market is between US$5 and US$10 billion. This number does not include
catastrophe and other insurance derivatives linked to mortality and
longevity; only property and casualty insurance risks are included.

The market has been growing, but the growth has not been steady. Similar to the
retro market (of which some consider this market a part), its size is particularly
prone to fluctuations based on the rate levels in the traditional
reinsurance market. The one part of the market that we can see growing is
that of exchange-traded insurance derivatives. However, exchange-traded
products are currently a relatively small part of the overall marketplace.

KEY INDEXES

A number of indexes have been used in structuring insurance derivatives
and ILW transactions. They include indexes tied directly to insurance losses
and those tied to physical parameters of events that affect insurance losses.
The overview below focuses on the indexes providing the most credible
information on the level of insured industry-level property losses due to
natural catastrophes.

Property Claim Services

PCS, a unit of ISO, collects, estimates and reports data on insured losses
from catastrophic events in the US, Puerto Rico and the US Virgin Islands.
While every single provider of catastrophe-insured loss data in the world
has at times been criticised for supposed inaccuracies or delays in reporting,
PCS is generally believed to be the most reliable and accurate.

In the half a century since it was established, the organisation has developed sound
procedures for data collection and loss estimation. It has the ability to collect,
on a confidential basis, data from a very large number of insurance carriers
as well as from residual market vehicles such as joint underwriting associations.
Other data sources are used as well. Insurance coverage limits, coinsurance, deductible amounts and other factors are taken into account by PCS in estimating insured losses. Estimates are provided for every catastrophe which is defined by PCS as an event that causes US$25 million or more in direct insured property losses and affects a significant number of
policyholders and insurers. Data for both personal and commercial lines of
business is included.

Loss estimates are usually reported within two weeks of the occurrence of
a PCS-designated catastrophe (and PCS provides the event with a serial
number). For events with likely total insured property loss in excess of
US$250 million, PCS conducts re-surveys and reports their results approximately
every 60 days until it believes that the estimate reasonably reflects
insured industry loss.

These larger events are the ones of interest for catastrophe
derivatives and ILWs. Figure 5.3 shows an example of PCS loss
estimates for Hurricane Ike at various time points, in reference to the settlement
prices for two of the exchange-traded catastrophe derivatives that use
PCS-based triggers.

While general catastrophe loss data is available dating back to the establishment
of PCS in 1949, the more detailed data by geographic territory and
insurance business line is available for only the more recent years.
In Table 5.1, opposite, we can see the development of industry-insured
loss estimates for the largest catastrophic events since 2001.

The time between the occurrence of a catastrophic event and reporting of the final
estimate could vary significantly depending on the event and complexity of
the data collection and extrapolation. Of the events shown in Table 5.1,
Hurricane Katrina had 10 re-survey estimates issued, with the last one
almost two years after the event occurrence.

However, the changes over the year preceding the reporting of the final estimate were minuscule. The 2008 Hurricane Gustav had the final estimate issued in less than five months,
with that final number not changing from the first re-survey estimate.

Insured loss estimates for catastrophes that happened before those shown
in Table 5.1 often lacked precision, even though they did not take longer to
obtain. For the 1994 Northridge earthquake in California, the preliminary
estimate increased 80% in two months, and the final estimate was five times greater than the original number.

However, we have to recognise the fact
that the methodologies employed by PCS have been changing; current estimation
techniques are more reliable given the possibly disproportionate
focus on the actual reported numbers years ago.

Catastrophe loss indexes based on PCS data are the basis for many ILW
and catastrophe derivative transactions, as well as for catastrophe bonds
and other insurance-linked securities. Both single-event and cumulative
catastrophe loss triggers can be based on PCS indexes.

 

Perils

Incorporated in 2009, PERILS AG was created to provide information on
industry-insured losses for catastrophic events in Europe, similar to the way
PCS provides information in the US. The plans call for ultimate expansion
of catastrophe data reporting beyond Europe to other regions outside the
US.

The shareholders of the company are major insurance and reinsurance
companies and a reinsurance intermediary, ensuring that a large segment of
catastrophe loss data will be provided to PERILS. The information is
provided anonymously by insurance companies and includes exposure data
(expressed as sums insured) by CRESTA zone and by country, property
premium data by country, and catastrophic event loss data by CRESTA zone
and by country.

The data is aggregated and extrapolated to the whole insurance
industry based primarily on known premium volumes. Industry
exposure and catastrophe loss data are examined for reasonableness and
tested against information from other sources. The methodology is still
evolving.

In December 2009, PERILS launched an industry loss index service for
European windstorm catastrophic events. The data can be used for industry
loss warranties (ILW) and broader insurance-linked securities (ILS) transactions
involving the use of industry losses as a trigger. Table 5.2 provides a
description of the PERILS indexes for ILS transactions.

ILW reinsurance transactions based on a PERILS catastrophe loss index
have been done shortly after the introduction of the indexes. The scope and
number of the indexes are expected to grow. The data collected by PERILS
will allow the company to create customised indexes for bespoke transactions.
The reporting is done in euros as opposed to US dollars.

Swiss Re and Munich Re indexes

The two largest reinsurance companies, Swiss Re and Munich Re, have been
compiling industry loss estimates for catastrophic events for decades. Swiss
Re’s sigma, in particular, has been compiling very reliable loss estimates for
catastrophe events worldwide, including manmade catastrophes. Munich
Re has assembled a very large inventory of catastrophic events in its
NatCatSERVICE loss database. It is similar to Swiss Re’s sigma in its broad
scope but does not include manmade catastrophes. Economic losses from
catastrophic events are often estimated in addition to the insured losses.
ILW transactions have been performed based on both Swiss Re’s sigma and
Munich Re’s NatCatSERVICE.

It is likely that for the windstorm peril Swiss Re’s and Munich Re’s estimates
are not going to be used for ILS transactions, since PERILS provides a
credible independent alternative. Other perils, and other regions around the
world usually do not have such an alternative, and it is likely that Swiss Re
and Munich Re indexes will continue to be used in structuring ILW and
other transactions. This practice may change in the future if PERILS implements
its ambitious expansion plans.

CME hurricane index

This index has been developed specifically to facilitate catastrophe derivative
trading. The index, based purely on the physical characteristics of a
hurricane event, aims to provide a measure of insured losses without the use
of any actual loss data such as reported industry losses. While the index has been developed
for North Atlantic hurricanes, in theory the same or a similar approach can
be used for cyclone events elsewhere.

Mortality and longevity indexes

A number of indexes tracking population mortality or longevity have been
developed for the express purpose of structuring derivative transactions.
These indexes are usually based on general population mortality as opposed
to that of the insured segment of the population. They can be used for
managing the risk of catastrophic mortality jumps affecting insurance
companies, or the longevity risk affecting pension funds, annuity product
providers and governments.

The CME hurricane index (CHI) was originally developed by reinsurance
broker Carvill and is still usually referred to as the Carvill index. CME Group
currently owns all rights to it.

The standard Saffir–Simpson hurricane scale is discrete and provides
only five values (from 1 to 5) based on hurricane sustained speed. Having
only five values can be seen as lacking in precision required for more accurate
estimation of potential losses. In addition, the Saffir–Simpson scale
does not differentiate between hurricanes of different sizes as measured by
the radius of the hurricane. Hurricane size can have a significant effect on
the resultant insurance losses. CHI attempts to improve on the
Saffir–Simpson scale by providing a continuous (as opposed to discrete)
measure of sustained wind speeds and by incorporating the hurricane size
in the calculation. The following formula is used for calculating CHI

V here is the maximum sustained wind speed, while R is the distance that
hurricane-force winds extend from the centre of the hurricane. The denominators
in the ratios are the reference values. V0 is equal to 74 m.p.h., which
is the threshold between a tropical storm and a hurricane as defined by the
Saffir–Simpson scale used by the National Oceanic and Atmospheric
Administration (NOAA) of the US Department of Commerce. The index is
used only for hurricane-force wind speeds, that is, for V equal to or greater
than 74 m.p.h. R0 is equal to 60 miles, which is a somewhat arbitrarily
chosen value intended to represent the radius of an average hurricane in the North Atlantic.

EQECAT is the current official calculation agent of the CHI for CME
Group. In calculating the value of the index used for contract settlement,
EQECAT utilises official data from NOAA. If some of the data is missing,
which would likely involve the radius of hurricane-force winds, EQECAT is
to use its best efforts to estimate the missing values. There are additional
rules governing the determination of which of the public advisories (from
NOAA) is to be used, what constitutes a hurricane landfall, and how
multiple landfalls of the same hurricane are treated.

There is also an index tracking mortality of a specific group of individuals
who have settled their life insurance policies, as opposed to the mortality of
the general population. Life-settlement mortality tracked by such an index
is very different from and not to be confused with mortality of the insured
segment of the population.

This article focuses on non-life insurance derivatives and ILWs.
Mortality and longevity indexes and the insurance derivative products
based on them are described in detail in the chapters dealing with securitised
life insurance risk and the hedging of longevity risk.

MODELLING INDUSTRY LOSSES

Modelling losses for the whole industry is performed using the tools that are
used for modelling losses for a portfolio of risks. Industry loss estimates are
significantly more stable than those of underwriting portfolios of individual
insurance companies. Data such as premium volume provides additional
information that assists in making better predictions.

In addition, using probabilistic estimates of industry losses is a natural way of comparing
different modelling tools. An outlier would be quickly noticed and need to
be explained. Expected annual losses for peak hazards produced by
different modelling tools do not significantly diverge. The overall probability
distributions, however, can differ considerably.

As an example, the following table shows estimated probabilities of insurance
industry losses, as would be calculated by PCS, from a single catastrophic
event exceeding a certain level that is used as trigger for catastrophe

derivatives and industry loss warranties. The probabilities do not correspond
directly to the results of any of the standard catastrophe models. The
assumption based on significantly heightened hurricane activity and warm
sea surface temperature is used instead of utilising the entire historical event
catalogue. This explains the higher than usually assumed probabilities of
exceedance.

THE ILW MARKET

The ILW market is very similar to the traditional reinsurance market in that
it is facilitated, almost exclusively, by reinsurance brokers. The three largest
reinsurance brokers, Aon Re, Guy Carpenter and Willis Re, account for
almost all of the market volume. There are several small brokers that participate
in the ILW market, but their share is small. Investment banks, despite
their role in ILS markets in general, have limited involvement in ILWs.

The vast majority of ILWs provide protection against standard risks of
wind damage and earthquakes in the US, wind in Europe and earthquakes
in Japan. All natural perils coverage for all of these territories is also
common. The US territory can be split into several pieces, of which Florida
has the most significant exposure to hurricane risk. In addition, second- and
third-event contracts are often quoted.

For these perils, in the US the standard
index is PCS losses, with trigger points ranging from as low as US$5
billion in industry losses to as high as US$120 billion or even greater to
provide protection against truly catastrophic losses.

Figure 5.1, opposite, illustrates indicative pricing for 12-month ILWs
covering the wind and flood risk in all of the US. The prices, expressed as a
percentage of the limit, are shown for first-event contracts at four trigger
levels: US$20 billion, US$30 billion, US$40 billion and US$50 billion. The
trigger levels are chosen to correspond to those used later in the chapter in
the illustration of price levels for the IFEX contracts covering substantially
the same catastrophe events.

The prices can be seen to fluctuate dramatically depending on the market
conditions. The highest levels were achieved following the Katrina–Rita–
Wilma hurricane season of 2005. Another spike followed the 2008 hurricane
losses combined with the capital depletion due to the financial crisis. The
expectations of even higher rates immediately before the hurricane season
of 2009, however, did not materialise.

Structuring an ILW

Industry loss warranties have become largely standardised in terms of their
typical provisions and legal documentation. A common ILW agreement will

be structured to provide protection in case of catastrophic losses due to a
natural catastrophe such as a hurricane or an earthquake.
The first step will be deciding on the appropriate index, which in the US
can be a PCS index. Once the index is chosen, the attachment point has to be
determined, as well as the protection limit.

As the value of losses from a
catastrophic event is not immediately known and an organisation such as
PCS will need time to provide a reliable estimate, a reporting period needs
to be specified to allow for loss development. This period can be, for
example, 24 months from the date of the loss or 18 months from end of the
risk term.

The contract risk term is generally 12 months or shorter. Some
ILWs provide protection only during the hurricane season. For earthquake
protection, the 12-month term is standard. Multi-year contracts are rare.
As an example of the legal language in a contract providing protection
against catastrophic losses due to an earthquake, the contract might “indemnify
the Reinsured for all losses, arising from earthquake and fire following
such earthquake, in respect of all policies and/or contracts of insurance
and/or reinsurance, including workers’ compensation business written or
assumed by the Reinsured, occurring within the territorial scope hereon.

This Reinsurance is to pay in the event of an Insured Market Loss for property
business arising out of the same event being equal to or greater than US$20 billion (a ‘Qualifying Event’). For purposes of determining the
Insured Market Loss, the parties hereto shall rely on the figures published
by the Property Claim Services (PCS) unit of the Insurance Services Office.”
The US$20 billion is specified as an example of the trigger level.

The limits can be specified in the manner typical of an excess-of-loss reinsurance
contract, with the possible contract language stipulating that the
reinsured will be paid up to a certain US dollar amount for “ultimate net loss
each and every loss and/or series thereof arising out of a Qualifying Event
in excess of” an agreed-upon “ultimate net loss each and every loss and/or
series thereof arising out of a Qualifying Event”.

A reinstatement provision
usually would not be included, but there are other ways to assure continuing
protection after a loss event, including purchasing second- or
multiple-event coverage, which can also be in the form of an ILW.
While the reinsurance agreement requires that both conditions be satisfied
– that is, only actual losses be reimbursed and only when the industry
losses exceed a predetermined threshold – the agreements tend to be structured
so that only the latter condition determines the payout.

The attachment point for the UNL is generally chosen at a very low level,
ensuring that exceeding the industry loss trigger level will happen only if
the reinsured suffers significant losses. There is, however, a chance of the
contract being triggered but the covered UNL being below the full reinsurance
limit.

Arguably the most important element of an ILW contract is the price paid
for the protection provided. The price would typically be expressed as rate
on line (RoL), that is, the ratio of the protection cost (premium) to the protection
limit provided. The payment is often made upfront by the buyer of the
protection.

An important issue in structuring an ILW is management of credit risk.
This topic is covered later in the chapter. Collateralisation, either full or
partial, might be required to assure payment. The need for collateralisation
is more important when the protection is provided by investors as opposed
to a rated reinsurance company.

ISDA US WIND SWAP CONFIRMATION TEMPLATE

In 2009, the International Swaps and Derivatives Association (ISDA)
published a swap confirmation template to facilitate and standardise the
documentation of natural-catastrophe swaps referencing US wind events.
Prior to that, several templates existed in the marketplace. The ISDA
template is based on the one originally developed by Swiss Re. The template
uses PCS estimates for insurance industry loss data for catastrophic wind
events affecting the US.

The covered territory is defined as all of the US,
including the District of Columbia, Puerto Rico and US Virgin Islands. The
option of choosing a subset of this territory also exists. It allows the choice
of three types of covered event: USA Wind Event 1, USA Wind Event 2 and
USA Wind Event 3. The first type is the broadest and includes all wind
events that would be included in the PCS Loss Report.

The second specifically
excludes named tropical storms, typhoons and hurricanes, while the
third includes only named tropical storms, typhoons and hurricanes. As in
all of the swap confirmations used in the past for US wind, flood following
covered perils is included in the damage calculation. The template clarifies
the treatment of workers’ compensation losses, and whether loss-adjustment
expenses related to such losses are included.

It allows for both binary
and non-binary (linear) payments in the event of a covered loss.
The ISDA template specifically states that the transaction is not a contract
of insurance and that there is no insurable loss requirement. The structure is
that of a pure financial derivative without any insurance component.
While the template brings legal documentation standardisation to these
OTC transactions, it allows a significant degree of customisation to minimise
the basis risk of the hedging party; this degree of customisation is not
possible when using only exchange-traded instruments.

IFEX CATASTROPHE DERIVATIVES

Of the exchange-traded catastrophe derivatives, IFEX event-linked futures
(ELF) are one of the two most common, the other being CME catastrophe
derivatives. IFEX is the Insurance Futures Exchange, which developed
(together with Deutsche Bank) event-linked futures. IFEX event-linked
futures are traded on the Chicago Climate Futures Exchange (CCFE), a relatively
new exchange focused on environmental financial instruments.

CCFE is owned by Climate Exchange PLC, a UK publicly traded company. The
founder of CCFE, Richard L. Sandor, played a key role in the introduction
of the first catastrophe derivative products in the early 1990s. Even though
the products were well designed, at the time the insurance industry was not
ready for such a radical innovation as trading insurance risk.

In addition to the need for education, the industry then did not have proper tools to quantify
catastrophe risk or to estimate the level of basis risk created by the use
of index-linked products as opposed to traditional reinsurance.
The CCFE IFEX contracts have been designed to replicate, as far as
possible, the better-known and accepted ILW contracts.

The two primary differences between a traditional ILW and the corresponding IFEX contract
are, first, that IFEX event-linked futures are financial derivatives and not
reinsurance, and, second, that IFEX contracts provide an effective way to
minimise if not eliminate the counterparty credit risk present in many ILW
transactions. The terms “IFEX contract” and “ELF contract” are often used
interchangeably.

Read More»

Catastrophe Model Structure

CATASTROPHE MODEL STRUCTURE

A catastrophe model that can be used in modelling insurance losses includes
all the primary elements mentioned above. It starts with generating a natural catastrophe event such as a hurricane or an earthquake, then determines its physical characteristics at the locations where insured properties
are situated, and finally determines the degree of damage caused to the properties and the total financial loss to the insurance companies.

The model effectively simulates many (sometimes as high as a million or
even more) hypothetical years and accumulates the loss statistics over these
hypothetical years. The large number of simulations is essential when
dealing with very rare events.

The basic structure of the catastrophe models has been described in this
and the previous chapter. Figure 4.16 shows a structure of a catastrophe
model that is designed specifically for the hurricane hazard; it also shows
some of the parameters that are generated by the model in intermediate
steps in order to arrive at the final result, aggregate financial loss.

Most (but not all) modules of the model are relatively independent of each
other, with one feeding its output into the next one. Each module is critical
in that it affects the end result to a significant degree. This structure explains
the need for the wide-ranging multidisciplinary expertise required for
developing such a model.

The distribution of aggregate insurance losses is the primary piece of
information used in the analysis of indemnity catastrophe bonds. A model
like the one outlined in Figure 4.16 also allows us to produce the probability
distributions of total industry losses or of catastrophic events without referencing
insurance losses, which are needed in the analysis of catastrophe
bonds with industry loss and parametric triggers respectively. Not all
elements of the model might need to be utilised in these cases.

MODELLING TERRORISM RISK

Modelling the risk of terrorist attacks has unique challenges not present in
modelling natural catastrophes. Similar to natural catastrophes, acts of
terrorism are represented by a sample of historical observations. However,
the applicability of such data to the present can be limited in that the political,
societal and technological landscape has probably changed since the
historical observations were made.

Until September 11 of 2001, our assessment of potential terrorist attacks was certainly different. In addition to the changing sociopolitical and technological landscape, there is also the human
factor of terrorists dynamically trying to choose the targets, weapons and
operational means of implementing an attack.
The article on securitising extreme mortality risk provides an overview
of how the risk of terrorism was modelled in some of the extreme mortality

bonds. In summary, the model developed by Milliman for those transactions
was based in part on a multi-level logic tree approach. At each level of
the logic tree, three choices were possible: “success” of the terrorist attack,
resulting in a random number of deaths in the predetermined range;

  “failure” of the terrorist attack; and escalation to the next level of severity
(greater number of deaths). The third choice led to the next level of the decision
tree, where the same choices were presented. At every level,
probabilities of each outcome – “success”, “failure” and escalation – were
determined by fitting a distribution to the actual observations over the
previous six-year period (that included 2001).

The model was simple and based on a very limited number of observations; however, it is not clear that more mathematically sophisticated models add value unless they are based
on additional external information.
The terrorism model described in the chapter on extreme mortality securitisation
focuses entirely on the risk of mortality due to acts of terrorism.
Property and other damage resulting from terrorism was not directly modelled.

Risk Management Solutions (RMS) has developed its own proprietary
terrorism risk model for the US, as well as a global model. The model is
based in part on the game theory approach to reflect changes in the landscape.
The situation is constantly evolving: as antiterrorism measures and
higher security are implemented, terrorists change their tactics and potential
targets. The moving target creates modelling difficulties that cannot be
addressed in a mathematical model but require extensive expert input. In
fact, this might be one of the cases where scenario analysis is preferable to a
fully probabilistic framework.

Using expert input is required to first build a database of potential targets.
Prioritising the targets is the next step; it requires the analysis of both the
target’s attractiveness to a terrorist and the degree of the target protection.
As the latter factors change, the priorities are adjusted as well. The database
of potential targets also contains data on potential damage to life and on
economic loss from a terrorist attack.

A terrorism model should also incorporate the fact of the existence of
several attack modes based on various weapons that could be used. In addition
to conventional weapons, chemical, biological, radiological or nuclear
(CBRN) weapons can be utilised, each with its own probability of occurrence
and potential damage.

The choice of terrorism weapons can also be site-specific, as some weapons would be more natural choices for attacks on specific sites. Finally, the mode of attack might be unconventional but it might not fit in the CBRN category either. The attack on the World Trade
Center in 2001 provides an example of such a type of weapon.

The RMS probabilistic terrorism model is a bold attempt to combine
rather sophisticated approaches taken from game theory, with extensive input on potential targets, threat levels and terrorist behaviour modes, in
order to quantify the risk of losses from terrorism, with the focus on large
losses that can be called catastrophic.

The input is dynamic in that the new developments such as antiterrorism measures, information on potential types of weapons that might be in the hands of terrorists, and even the level
of “chatter” detected by the intelligence community can in theory be
reflected in the inputs into the model or in adjusting some of its parameters.
The overall framework appears to allow a growing degree of sophistication
and the incorporation of additional information on a dynamic basis.

The practical implementation, however, presents numerous challenges.
In assessing a difficult-to-quantify risk such as terrorism, it is particularly
important to augment the probabilistic approach with scenario analysis.
Along with allowing for reasonability testing, scenario analysis introduces
one more way to use expert judgement in analysing exposure to the risk of
terrorist attacks.

MODELLING PANDEMIC FLU RISK

The risk of a global pandemic of an infectious disease is not insignificant.
The chances of a pandemic of a serious disease with a high level of mortality
might be small, but the consequences of such an event would be catastrophic.
Focusing on insurance losses, there would be a spike in mortality rates resulting in life insurance losses of possibly a catastrophic nature, as well as an avalanche of medical claims resulting in huge health insurance losses.

The latter might be the case even if the mortality rate is not high but
the severity of the disease is. Finally, there would be property-casualty
insurance losses. These would obviously include business-interruption
insurance losses. However, it is possible that other lines of property-casualty
insurance business might suffer even greater losses, even though such losses
are usually not fully contemplated in catastrophe risk analysis.

The chapter on extreme mortality bonds describes how pandemics have
been modelled in the context of evaluating their potential impact on
mortality rates resulting in a mortality spike. In analysing the risk of
pandemics, the main focus is flu pandemics, since these are considered to
represent the great majority of this type of risk in modern times.

Milliman created a model for analysing the risk of mortality spikes due to flu pandemics in catastrophe mortality bonds. The model separated the frequency and severity components, parameters of which were estimated based on the available historical data. The data for
frequency was considered over a long (multi-century) period of time, at least in some cases. Binomial distribution was used for annual frequency, which is a natural choice in modelling the frequency of such events.

Severity data was based on five or six data points in the more recent history. In at least one
of the securitisations, Milliman modelled severity as a percentage of excess
mortality fitted to these historical data points, one of which was adjusted by
placing a cap on broad mortality improvements in the general population.
(See the fitted severity curve for excess mortality resulting from pandemics
for the Tartan Capital securitisation, in the chapter on the securitisation of
extreme mortality risk.)

The Milliman model then simulates the pandemic
results by sampling from the frequency and severity distributions. The
current Milliman model’s results are sensitive to the distribution of age and
gender. The binomial frequency distribution assumes that the probability of a
pandemic is the same in any year. It is likely that the current risk of a flu
pandemic is elevated above the average historical levels.

This can be reflected by adjusting the mean of the binomial distribution; significant
judgement and expert input are required to properly make this adjustment.
The Milliman model is of the type that is sometimes called actuarial, in
that frequency and severity are modelled separately based on available
historical data. Another approach – the epidemiological one – is used in the
model developed by RMS.

It is based on a standard epidemiological approach known as SIR modelling (susceptible, infectious, recovered), which allows us to take into account additional variables such as vaccination, immunity, viral characteristics and lethality in a more direct way. The
RMS model presents a more sophisticated approach from the mathematical
point of view; but whether it is better than the simpler Milliman model is not
fully clear, since it requires a number of inputs that introduce uncertainty
and have the potential to skew the results. In the longer term, however, the
RMS model is likely a better one to use for modelling pandemic risk.

The Swiss Re internal model is reported to be a combination of the actuarial
and epidemiological types. The excess mortality rates are estimated
based on historical data as in the Milliman model, but are then adjusted to
take into account the changes that have happened since those observed
events. These changes include new virus threats, vaccinations, better standards
of medical care, etc. A significant degree of judgement is used in
making these adjustments.

The article on securitisation of extreme mortality risk shows a fully
stochastic model of the spread of a pandemic, implemented on the Los
Alamos National Lab supercomputer. This approach is probably the one that will eventually become the standard. Right now it is not realistic. Of the
models described above, the RMS model is the closest to this approach.

PRACTICAL MODELLING OF CATASTROPHE RISK

It is not certain that everything is uncertain.
Blaise Pascal

The time of occurrence of a natural catastrophe is unpredictable. Its magnitude
is unpredictable too. So is the damage it causes in its wake. This is the
inherent uncertainty associated with such events as hurricanes or earthquakes.
When it comes to natural catastrophes, we are in the country where
predictions do not work.

Manmade catastrophes are in the same territory. The goal of modelling catastrophic events in the context of insurance securitisation as well as in general is to minimise the uncertainty
surrounding the probability distribution of possible outcomes. The closest to
certainty is the one who most precisely identifies and quantifies the uncertainty
of these random variables.

Available models

The previous chapter identified the three main providers of commercial
catastrophe-modelling software used in the analysis of potential insurance
losses. In addition to AIR Worldwide, EQECAT and Risk Management
Solutions, there are additional providers of either software or consulting
services based on proprietary software for modelling of catastrophic insurance
losses.

These tend to focus on one type of hazard in a specific
geographic area. For example, Applied Research Associates’ hurricane
model and URS’s earthquake models (combined and modified under the
Baseline Management umbrella) are now covering all of the US. There are
also some noncommercial models such as the Florida Public Hurricane Loss
model (for Florida hurricane risk only) and FEMA’s HAZUS tool, which in
its modified form can be used for modelling insurance losses.

While a number of external models exist, in practice only the main three,
AIR Worldwide, EQECAT and Risk Management Solutions, have been
utilised in securitisation of insurance risk. This is reflective of the complete
domination of these three companies in the insurance and reinsurance
industry and the credibility they have earned over the years.

Problems – realor perceived – with modelling software developed by these companies have
been pointed out on a number of occasions. However, they do have the track
record and credibility that no competitor possesses.
Some companies in the industry, in particular reinsurance companies, have developed their own proprietary models of insurance catastrophe risk.

However, these are generally not full catastrophe models but rather the software
that sits on top of the three established models and uses their output
to obtain its own estimate, which might be different from the results of each
of the underlying models.

While not every peril in every geographical area can be modelled, there
now exist catastrophe models covering all the key areas of insurance exposure.
Table 4.5 shows an incomplete list of the existing peril models and the
countries for which they have been created. In almost all circumstances, all
three major modelling companies would have these models.

While many individual models – for specific perils and countries – are
available, not all of them have the same degree of credibility. Models for
some regions and perils are based on more extensive research and have
existed for a longer period of time. The longer period of time has created
more opportunities for model validation and refinement. Not surprisingly,
the three most refined models cover:

1. North Atlantic hurricanes (in particular Florida and the other Gulf
states in the US);
2. California earthquakes; and
3. Japanese earthquakes.

These three represent the biggest catastrophe risks for the insurance
industry. They combine high concentration of insured exposure and high
probability of catastrophic events. Even though the models produced by the
three modelling firms have existed for a long time, their results differ, sometimes
significantly, from one firm to another, and significant adjustments to
each of them have been made even very recently.

The net result is the uncertainty that still exists in quantifying catastrophe insurance exposure
even in the areas where the research has been extensive and the investment
in model development quite sizable.

It is important to carefully analyse whether indirect effects of natural
catastrophes have been modelled, and, if so, how. These indirect effects
include, for example, flood following a hurricane and fire following an
earthquake. These secondary effects might result in more damage than the
primary ones, and their proper modelling is critical.

Unmodelled losses

One of the most common examples of unmodelled losses are those that
reflect improper data coding, resulting in wrong or incomplete entry of

Period	Peril	Country+
Hurricanes, cyclones and storms	North America, Mexico and Caribbean	US (including Alaska), Mexico, Bahamas, Barbados, Bermuda, Cayman Islands, Dominican Republic, Jamaica, Puerto Rico, Trinidad and Tobago
	Europe	Austria, Belgium, Denmark, France, Germany, Ireland, Netherlands, Norway, Sweden, Switzerland, UK (including flood)
	Asia-Pacific	Australia, China (including Hong Kong), Hawaii (US), Japan, Philippines, Taiwan
Earthquakes	North America, Mexico and Caribbean	US (including Alaska), Canada, Mexico, Bahamas, Barbados, Cayman Islands, Dominican Republic, Jamaica, Puerto Rico, Trinidad and Tobago
	Central and South America	Belize, Chile, Costa Rica, Colombia, El Salvador, Guatemala, Honduras, Nicaragua, Panama, Peru, Venezuela
	Europe and Middle East	Greece, Israel, Italy, Portugal, Switzerland, Turkey
	Asia-Pacific	Australia, China, Hawaii (US), Indonesia, Japan, New Zealand, Philippines, Taiwan
Tornado and related	North America	Canada, US
Terrorism	North America	US (worldwide terrorism models also exist but their credibility level is unclear)
Flu pandemic	Worldwide	Worldwide

exposure into the model. This is part of the pervasive issue of data quality
described below.
It is not unusual for some of the insured exposure not to be reflected in the
models because they are not designed to handle specific types of coverage.
Additional perils, related to the main one but in an indirect fashion, would
probably not be taken into account by the model.

Finally, there might be insurance losses due to catastrophic events that have never been contemplated in the original coverage but still have to be paid by insurance
companies. Care should be taken to make sure that all losses that can be
modelled by catastrophe software are input, and any other losses evaluated
separately.

The issue of data quality is usually raised not in the context of the data
used to formulate and parameterise the models, but in assessing the reliability
and completeness of the data on the details of the exposure in applying
a catastrophe model to a portfolio of insurance policies. 

Quality of the insurance data serving as input into catastrophe models is an industry-wide issue
introducing a significant degree of uncertainty to results of the modelling
process. Best practices are still in the process of being developed, and the
quality of data can vary widely from one insurance company to another.
Improper data coding or not capturing all the relevant exposure data in
sufficient detail is also an indication of deficiencies in the underwriting
process.

Implications for investors can be significant. Two insurance-linked securities,
such as catastrophe bonds with indemnity trigger, might appear very
similar but in reality have different risk profiles because of the different

Modelling results presented to investors

As a reminder of the primary goal of the analysis, Panel 4.4 shows the
summary output of the risk analysis performed for an indemnity catastrophe
bond (see the chapter on property catastrophe bonds for additional
information). It is no more than a summary, but it is often the main part of
the information included in the offering circulars, no matter how long the
risk analysis section appears to be.

DATA QUALITY

The quality of data used in catastrophe models is as important as the quality
of the models themselves. Data used to create and parameterise the models
affects the precision and correctness of modelling results. Many elements of
the existing models have been built so that they can take advantage of the
most reliable data available. For example, certain hurricane data available
from the National Oceanic and Atmospheric Administration databases
include measurements at six-hour intervals. Models have been constructed
specifically to take the six-hour intervals into account, as other data is either
unavailable or not fully reliable. This is also the data used to validate the
models.

ILLUSTRATIVE SUMMARY OUTPUT OF RISK ANALYSIS OF A CATASTROPHE BOND

A simplified catastrophe bond description is presented below. The
coverage attaches at US$5 billion of ultimate net loss resulting from a single
occurrence of a hurricane.

Transaction parameters

Covered risk :                               Hurricane affecting specific insurance portfolio
Trigger:                                         Indemnity per occurrence (UNL)
Attachment:                                  level US$5.0 billion
Exhaustion:                                   level US$5.5 billion
Insurance percentage:                 50%
Principal amount:                        US$250 million

Based on the per-occurrence exceedance probabilities resulting from catastrophe
modelling of the subject insurance portfolio, key risk measures are
calculated. The expected loss in this example is 1.48% per annum. The
attachment probability is 1.70%.

Risk measures	Base case  (standard catalogue) (%)	Warm Sea Surface Temperature catalogue (%)
Attachment probability	1.70	2.54
Exhaustion probability	1.30	1.83
Expected loss	1.48	2.15

In this example, modelling was done twice: first with parameterisation
based on the long-term historical averages of hurricane activity in the
covered territory, and then based on the so-called Warm Sea Surface
Temperature catalogue to take into account the greater chance of hurricane
activity in the current period. The latter is of most interest since it is believed
to present results that are more realistic.

This summary does not include many of the other important elements of
risk analysis. However, it does show the two figures of most interest to
investors: expected loss and attachment probability. Expected loss provided
in the offering circular serves as the starting point for analysis performed by
investors.

degrees of uncertainty related to data quality and underwriting standards in
general. In evaluating such insurance-linked securities, the few investors
familiar with underwriting processes of individual insurance companies can
have an advantage over those not possessing this level of expertise.
The seemingly inconsequential issue of data quality can play a much
greater role in modelling catastrophe risk than we would expect. It presents
a good illustration of the “garbage in, garbage out” principle, and could be
an important element of the analysis performed by investors.

INVESTOR AND CATASTROPHE MODELLING

Investors in catastrophe insurance-linked securities are presented with
numerous choices and decisions in their analysis. Most of them have been
mentioned or alluded to above.

The questions to be answered are numerous. Which catastrophe model is
most appropriate for a specific type of risk exposure? How different are the
results of different models? Are there known biases in some models related
to specific perils or geographical regions? Are models for one region more
credible than for another?

How can we quantify the additional uncertainty
related to the lower credibility of some models? Are there ways to validate
some modelling results? What are the primary sources of uncertainty in the
modelling? How do we quantify the additional uncertainty of securities
with indemnity as opposed to parametric trigger?

The list of questions never ends, which once again underscores the advantages
of having modelling expertise in the analysis of insurance-linked
securities. It almost makes us wonder whether the informational disadvantage
of the investor is too great to play the ILS game. The disadvantage is
relative to both the sponsors of catastrophe bonds and to reinsurance
companies that often invest in these securities. Both seem to have the level of expertise that an investor is usually unable to achieve.

The answer to this question is more optimistic than it appears to be, however. Investors can and
do participate in this market and generate attractive risk-adjusted returns.
While reinsurance companies in their role as investors seem to have some
expertise that few investors possess, it is not necessarily the type of expertise
that is most important in ILS investing.

Investors have the capital markets outlook that is usually lacking in insurance and reinsurance companies investing in insurance-linked securities. This capital markets view gives
investors an advantage in some areas even when they are disadvantaged at
others. Ultimately, the conclusion is simple: modelling is critical, and without modelling expertise it is impossible to generate high-risk adjusted returns
on a consistent basis. The industry is slowly coming to this realisation.
Managing catastrophe risk on a portfolio basis is one of the most critical
elements of ILS investing. The choice of modelling tools is now available for
this purpose; it is also discussed in the chapter on modelling portfolios of
catastrophe insurance-linked securities.

CATASTROPHE BOND REMODELLING

Almost every cat bond transaction has involved the analysis performed by
one of the three main modelling agencies, AIR Worldwide, EQECAT and
RMS. The summary of the analysis is included in the offering documents; a
data file such as an Excel spreadsheet might also be provided as part of the
offering circulars.

This raises the question of the differences between
models. The annual expected loss or probability of attachment calculated by
AIR Worldwide might differ, perhaps significantly, from the annual
expected loss or probability of attachment if they were calculated by one of
the other models based on the same data.

Leaving aside for a moment the question of which model is “better”, in
the ideal world an investor would like to see the analysis performed by all
three modelling firms and then make their own conclusions. “Remodelling”
refers to analysing a catastrophe bond by a modelling firm that did not
perform the initial analysis that was included in the offering documents and
used in pricing of the bond.

If the security has a parametric trigger, all the
data is available and another modelling firm can easily perform its own
analysis so that the results can be compared. Comparison is much more
difficult for indemnity catastrophe bonds. For these bonds, it is necessary to
have full exposure information in order to perform the analysis. Such information
is never provided to investors; only summaries are included in the
offering circulars.

In order to perform the analysis, in this situation another modelling firm
has to make a choice between two simplifying assumptions. One of them is
to assume the correctness of the analysis, such as the values of expected loss,
attachment probability and the exhaustion probability. Based on these
figures and the exposure summary in the offering circular, the modeller then
tries to work back to the inputs to arrive at exposure expressed at a greater
level of detail than is provided in the documentation.

The exposure information is important in portfolio management, where it allows us to monitor
exposure accumulation over many securities and properly establish the
risk–return tradeoffs on a portfolio basis.

Another choice would be to start with the exposure summary in the
investor documents, and try to estimate what the exposure is at a more
detailed level. This could be done by supplementing the exposure data
provided with publicly available data on the geographic and line-of-business
distribution of exposure for the sponsor, as well as the possible
knowledge by the modeller of the underwriting processes of the sponsor.

The resultant expected loss and the exceedance probability would then
differ from those in the offering circular. This type of analysis can now be performed very fast, even during the initial marketing stage before the bond pricing has been finalised. This topic
is revisited later in greater detail.

HURRICANE FORECASTING

“Hurricane forecasting” refers to probabilistic predictions of hurricane
activity in the short term. These are not actual forecasts but probability
distributions of potential outcomes based on the most current data. These
forecasts refer to the upcoming hurricane season or a season already in
progress.

William Gray, for all intents and purposes, pioneered the field of hurricane
forecasting. He developed a number of forecasting methodologies with
a special focus on North Atlantic hurricanes. Phil Klotzbach, who has taken
from him the leadership of the hurricane forecasting project, in 2009 started
issuing 15-day forecasts in addition to the seasonal ones.

This is a big change from issuing forecasts from the one to five times a year common for hurricane forecasters. The Klotzbach/Gray group has proven its skill over the
years of issuing hurricane forecasts for the North Atlantic. Its methodology
is continuing to evolve, but in most general terms it is based on identifying and monitoring several atmospheric and/or oceanic physical variables,
either global or relatively localised, that are relatively independent of each
other and have been shown, by utilising statistical analysis tools, to serve as
good predictors of the following North Atlantic hurricane season.

NOAA issues hurricane forecasts too, as do several research groups
around the world. It appears that as of 2009 only the Klotzbach/Gray group
has been able to clearly demonstrate its skill in forecasting probability of
major hurricane landfalls in the US.

Other groups either do not issue forecasts associated with landfalls or have not been recognised for their skill in successfully forecasting landfalls. In insurance catastrophe modelling, landfalls
are of major importance, while hurricanes that bypass land are of
interest only if they have the potential to damage oil platforms.

The forecasts create additional opportunities for optimising risk-adjusted
return on a portfolio basis. They also provide input into pricing of all
affected insurance-linked securities, and in particular ILWs, securitised reinsurance
and catastrophe bonds close to expiration.

Live cats

The term “hurricane forecasting” is also used in reference to probabilistic
assessment of development of the storms and hurricanes that have already
formed and might make a landfall. The ability to trade the risk of natural
catastrophic events that can occur in the very near future – from several days
to several hours – creates opportunities for those who can obtain better
information on the projected path and potential damage from the hurricane
and to better take advantage of the situation. It also creates opportunities to
offload excess risk if necessary.

This “live cat” trading can be done on a more
intelligent basis when short-term hurricane forecasts have a relative degree
of credibility.

The topic of hurricane forecasting is revisited in the chapters on ILWs and
catastrophe derivatives and on managing investment portfolios of insurance
catastrophe risk.

CLIMATE CHANGE
The trouble with our times is that the future is not what it used to be.
Paul Valéry

Climate change has been mentioned more than once in the context of modelling
catastrophe risk. The expectations of the future climate state are
different from its current one. The effects of climate change relevant to hurricane
activity, in particular the increase in sea-surface temperature, can
already be observed. These changes make it harder to rely on the old
approach of forming conclusions about future natural catastrophe activity
based entirely on prior historical observations.

The future frequency and severity of hurricane events might be a function of atmospheric and oceanic processes that are different from the ones in the period of historical observations.
The focus of an investor in the analysis of insurance-linked securities tied
to the risk of natural catastrophes is on the relatively short time horizon.
Changes expected to take place over a long period of time are of less significance
due to their minimal impact on catastrophe-linked securities that
tend to have short tenor.

Unless there is a clearly observable trend, this view
suggests disregarding recent changes and relying primarily on the longterm averages of hurricane frequency and severity. If the speed of the
climate change is rapid, though, this view might be incorrect; there is a need
also to reflect the developing new environment in evaluating the risk of
future hurricanes. In addition, it is possible that the climate changes have
already altered the atmospheric and oceanic processes, probably starting a
number of years ago.

This view would necessitate immediately taking
climate change into account. In simple terms, we can then see the observed
historical sample of hurricane activity as consisting of two parts: the first,
longer, period when the conditions were relatively constant and the variability
was due to natural statistical fluctuations; and the second period
encompassing more recent years when a trend might be present in the
changing atmospheric and oceanic conditions that influence hurricane
activity. The trend might be accelerating, as suggested by all of the global
warming theories.

The decision regarding whether we are in the period of heightened hurricane
activity and whether this activity is likely to accelerate in the very near
future is an important one both for insurance companies with significant
hurricane risk accumulation and for investors in catastrophe insurancelinked
securities. The majority have decided that we are now in a period of
climate change that has higher probability of hurricane activity than
suggested by long-term historical averages.

The modelling firms have incorporated this approach by creating an option in their software models to allow users to make their own choice about whether to base the analysis on
long-term averages or assume higher levels of hurricane activity than
suggested by the history. The latter option is referred to as using the Warm
Sea Temperature Conditioned Catalogue of events when no additional
trends are taken into account.

The decision to use higher levels of potential hurricane activity as the
primary modelling approach is not tied directly to the acceptance of the
global warming theory; as mentioned earlier, the shorter-term climate
processes of an oscillating nature can provide a sufficient reason for
believing we are in an environment more conducive to hurricane development
than in the past.

SPONSOR PERSPECTIVE ON MODELLING

The importance of catastrophe modelling for insurance and reinsurance
companies is apparent. Modelling catastrophe insurance risk is part of the
enterprise risk management (ERM) process. Its results are used in making
decisions on the best ways to employ company capital. They are an important input in decisions on whether to retain the risk, reinsure some of it or
transfer it to the capital markets.

The transfer to the capital markets can be
in the form of sponsoring insurance-linked securities such as catastrophe
bonds or in the form of hedging catastrophe exposure by purchasing ILWs
or catastrophe derivatives. Another option available to insurance and reinsurance
companies is to rebalance or reduce their underwriting to lower the
overall exposure to catastrophe risk.

For companies writing insurance that creates catastrophe exposure,
modelling the risk of catastrophes is part of the standard business processes
of underwriting and risk management; it is used also in capital allocation.
Facilitating risk securitisation is not the primary goal of catastrophe modelling,
even though the decision to transfer some of the risk to capital markets
might be based on the modelling results. Instead, the emphasis is on total
risk exposure.

Modelling catastrophe risk is growing in importance at insurance
and reinsurance companies, as management see the benefits it delivers.
Quantification of catastrophe risk exposure is also driven by shareholders
and rating agencies. Regulators are also paying more attention to catastrophe
risk than ever in the past.

It would appear that the insurance industry has greater expertise in
modelling catastrophe risk than the investor community. While this is
generally true, there are investors who are very sophisticated in catastrophe
modelling, while the insurance industry expertise is generic and not focused
on the specific issues relevant to securitising insurance risk.

MODELLING AS A SOURCE OF COMPETITIVE ADVANTAGE TO INVESTORS

The primary risk of insurance-linked securities in almost all cases is, of
course, the insurance risk. The risk of catastrophic events is the one most
commonly transferred to investors; on the property insurance side the risk
of catastrophic events fully dominates insurance securitisation. To make an
informed decision, an ILS investor has to understand the risk profile of these
securities.

Without this understanding, it is impossible to make any intelligent
decisions on individual insurance-linked securities or their portfolios.
Catastrophe modelling and the risk analysis based on it are key to understanding
the risk profile of these securities.

(As pointed out earlier, there might be situations when an investor makes an informed decision to allocate a small portion of their assets to insurance-linked securities without developing
expertise in this asset class. These situations are rare.)

Since the ability to quantify risk and determine its proper price is based on catastrophe modelling and risk analysis, those investors better able to
understand the risk analysis section of the offering circulars for catastrophe
bonds have an immediate advantage over the rest of the investor community.
Properly interpreting the risk analysis section requires knowledge of
modelling techniques used, modelling software packages utilised, model
credibility, the way exposure data is captured, and other modelling-related
issues.

Those who have better understanding of these issues have an advantage
over those who do not. They are in a better position to quantify the
uncertainty, make adjustments if necessary, and extract more useful information
from the same risk analysis section of the offering circulars. This
advantage is not limited to catastrophe bonds and is applicable to all types
of catastrophe insurance-linked securities.

Finally, those investors who use catastrophe modelling tools themselves
have an extra advantage over those who do not. They tend to have a greater
degree of understanding of the assumptions underlying the models and the
types of uncertainty involved. The most sophisticated of them are able to
perform additional sensitivity analysis and scenario testing, to come up with
a better understanding of the risk profile of the security and the price to
charge for assuming this risk.

An example of the competitive advantage held by those with superior
understanding of catastrophe modelling tools can be found in the analysis
of California earthquake exposure. The difference in scientific views on
which part of the San Andreas fault is most ripe for a major earthquake
(referred to earlier in this chapter) is one of the reasons for the divergence in
results among commercial catastrophe models in estimating expected losses
at various exceedance levels from one part of California to another.

(The divergence is true at the time of writing; models evolve, and updates and
new releases are issued periodically.) Understanding the difference between
models is by itself a source of competitive advantage; having an informed opinion on which model is likely to produce more precise results for a
specific peril and geographical territory adds significantly to this competitive
advantage.

Even an informed view on the likely variability of results
around the expected mean for a specific peril and geographical territory,
and how it varies from model to model, is an informational advantage.
The use of models by investors is of particular importance in portfolio
management.

Without using real catastrophe models, all an investor can do
is to make very rough estimates of the risk accumulation by peril/geography
bucket and try to put limits on individual risk buckets. There is no
way to properly estimate risk-adjusted return for the portfolio, or how the
addition of a position will affect the overall risk–return profile. The investors
who are able to use modelling tools, both in the analysis of individual securities
and in portfolio management, have an important competitive
advantage, the value of which is magnified by the overall inefficiency of the
insurance-linked securities market.

MODELLING AS A SOURCE OF COMPETITIVE DISADVANTAGE TO INVESTORS

The appearance of models designed specifically for investors in insurancelinked
securities such as catastrophe bonds is changing the way some
investors are approaching ILS investing. Some of those who never utilised
catastrophe modelling tools before have now tried to use the new software
to model their ILS portfolios.

The models designed specifically for investors
are described elsewhere, including in the chapter on portfolio management.
They are much simpler to use and understand than the full-blown catastrophe
models used by insurance companies and, in most cases, by
modellers providing the risk analysis in structuring catastrophe bonds. They
do provide ways to analyse and visualise portfolio exposure, perform “what
if” analysis, and more. They appear to be simple to use.

The seeming simplicity of the tools is deceptive, however. By themselves
they do not provide more than a software platform to combine individual
cat bonds into one portfolio, with a semiautomatic way of calculating
several risk measures.

This platform is very useful to those who already
understand the modelling approaches, the assumptions used in modelling,
the differences between the models used for initial analysis, the degree of
possible unmodelled risk, and many other factors required for using modelling
tools and properly interpreting modelling results.

For others, not possessing this expertise, the picture might be different. The availability of a
tool that is a black box to a user can have mixed consequences. The tools
themselves are not true black boxes: they are black boxes only to those who
do not have the requisite expertise to use them effectively.

While most ILS investors do not use these portfolio management tools,
some of those who do may be worse off than if they did not. The ability to
see all securities in one portfolio and have the software spit out risk
measures and other statistics can create the illusion of understanding and
properly managing portfolio risk when none is present.

Modelling can be very dangerous to investorswho lack the understanding
of howit is performed andwhat the resultsmean.Of course, the danger is not
in modelling, but in not having the level of expertise needed to understand
the modelling methods, output and implications. This problem has existed
for a very long time and is unrelated to the appearance of software tools
targeted specifically at the ILS investor.

Improper interpretation of the risk analysis section of offering circulars by some investors has been going on for so long because of the seeming simplicity of the data presented. It creates the
illusion of understanding, and that can be very dangerous. Some investors
have become proficient in the lingo of catastrophe bonds and relatedmodelling
but,without realising it, have not gained the level of expertise needed to
turnmodelling into a useful tool. To think they understand the risk of securitieswhen
they really do not creates a dangerous situation.

The false sense of security when it comes to risk management, and the
illusion of actively managing a portfolio to maximise its risk-adjusted
return, can lead to catastrophic results for some investors in catastrophe risk.
One more danger to point out is that the investors focused on modelling
catastrophe risk are sometimes focused on it too much, to the degree that
they do not pay the necessary attention to other types of risk associated with
insurance-linked securities.

These other risks are important in the analysis of
individual securities; it is also important to take them into account when
these securities become part of an investment portfolio.

The problems mentioned above would become obvious and self-correct
in investing in almost any other asset class. The level of historical returns
and their volatility by itself would be a clear indicator of investor expertise,
in most cases. Catastrophe ILS are tied to the risk of very rare events, and a
track record of several years says little about the level of risk-adjusted
returns generated.

TRENDS AND EXPECTATIONS

The importance of modelling in the analysis of insurance-linked securities is
impossible to overestimate. The specific type of modelling involved in the
probabilistic analysis of catastrophe events and the resulting insurance
losses is unusual in the investment world and requires specialised expertise.
The times when most investors made their decisions based on the rudimentary
analysis of the information in the offering documents have passed. A
greater level of sophistication is now required.

Insurance and reinsurance companies seeking to transfer some of their
risk to the capital markets in the form of insurance-linked securities
have dramatically improved and continue to improve their risk modelling
and management. They are more and more finding themselves in the position of being able to make fully informed decisions on the ways
to manage their catastrophe exposure and properly choose among such
options as reinsurance, securitisation and retaining catastrophe risk.

• Superior modelling skills and the ability to better interpret results of modelling catastrophic events are a major source of competitive advantage to the investors who have this level of expertise. As the importance of modelling is becoming more widely recognised, those who lack the expertise will find it increasingly difficult to compete effectively.
• The ability to model risk is particularly valuable in assembling and managing portfolios of insurance-linked securities. This skill is even more important at the portfolio management level than in determining the right price for a particular catastrophe bond or another security whose risk is linked to catastrophic events.
• Without models, it is impossible to assess the risk-adjusted return in investing in catastrophe-linked securities. Without understanding the risk profile of a security, investors are in no position to evaluate whether they are being properly compensated for assuming the risk.
• Track record of a fund investing in insurance-linked securities can often be meaningless and even misleading. Some of the investors who have been most successful on paper have achieved higher returns by taking on disproportionate amounts of risk, often unknowingly. Without properly utilised models, we cannot analyse this type of risk. When investing in the more traditional asset classes such as equities, track record of returns is usually very informative and revealing; but it is of less importance in investing in insurance-linked securities and can be considered only in the context of the risk that has been taken. Catastrophic events are, by their very definition, very rare, and it is possible for an investor to “be lucky” for quite a long period of time even when the investment portfolio is completely mismanaged.  advantage for an investor in insurance-linked securities. It also enables better decision making for sponsors in dealing with the issues of basis risk.
• Issues of data quality, understanding model limitations, credibility of models, and biases among existing models are key components of the type of expertise that can provide a competitive advantage.
• Important as the use of modelling tools is, better understanding of the assumptions and superior interpretation of the results are of even greater significance. These two can be the most important sources of competitive advantage.

This article provided but an introduction to selected concepts in modelling
catastrophic events in the context of analysing insurance risk securitisation.
Some additional information on the topic can be found in other post in this blog.
The issues touched on here should provide an understanding of why modelling
catastrophe risk is important and why it is so difficult.

Read More»

Modelling Catastrophe Risk Part 2

SEASONALITY OF THE HURRICANE RISK IN INSURANCE-LINKED SECURITIES

The main hurricane risk of insurance-linked securities, that of North Atlantic hurricanes, is seasonal as opposed to following uniform distribution. The hurricane season officially starts on June 1 and ends November 30. Very few hurricanes occur outside the hurricane season. Approximately 97% of all tropical storm activity happens during these six months.

As the the above diagram, there is a pronounced peak of activity within the
hurricane season, which lasts from August through October. Over three quarters
of storms occur during this period. The percentage of hurricanes, in
particular major hurricanes, is even greater: more than 95% of major hurricane
(Category 3 and greater) days fall from August through October.

Definition of hurricane season is rarely used in the offering documents for
insurance-linked securities. Instead, specific dates determine the coverage
period. Knowing when the hurricane season officially starts and ends is not
relevant. However, there are some insurance-linked securities for which the
definition of the hurricane season is important. Exchange-traded IFEX catastrophe
futures use a formal legal definition of North Atlantic hurricane season.

This definition is used in establishing maintenance margin levels for
IFEX contracts. Catastrophe futures and similar insurance-linked securities
are described in detail in other chapters.
Hurricanes threatening the Pacific coast of the US and Mexico have a
longer period of heightened activity, which starts earlier than on the Atlantic
coast but has the same activity peak as the North Atlantic hurricanes. West
Pacific hurricanes are distributed even more evenly over the year; they are
less important in securitisation of insurance risk.

Hurricanes in the Southern Hemisphere (called typhoons or cyclones
there) tend to occur between October and May, but specific frequency distributions
depend on ocean basin.

LANDFALL FREQUENCY IN PEAK REGIONS

Returning to the North Atlantic hurricanes, which present the greatest
threat in the southeastern US, The following two figures  illustrate hurricane
landfall frequencies expressed as return periods. Unlike the figures
above, only landfalls – which typically are the only hurricane risk in insurance-
linked securities – are shown, with the two graphs corresponding to
hurricane Categories 1 and 5 on the Saffir–Simpson hurricane scale.

Return period is defined here as the long-term average of a recurrence
interval of hurricane landfalls of specific or greater intensity (category) at the
time of landfall. It can also be seen as the inverse of the annual exceedance
probability. Return period is usually measured in years.
Historical data is the best indicator of future hurricane frequencies. Of
course, this does not mean that a simple sampling of the historical frequencies
should be used in hurricane simulations. It means only that historical
data is the starting point of any model, which is also where we return to validate
the model once it has been built. A sound model is much more than just
fitting of a distribution to the existing data points; some extremely sophisticated
models have been created in recent years.

HURRICANE FREQUENCY AND SEVERITY EFFECTS OVER VARIOUS
TIME HORIZONS

Continuing to focus primarily on hurricanes affecting the US, three primary
phenomena affect hurricane frequency and severity, each operating over its
own time scale: short term, medium term and medium to long term.

1 Short term

ENSO, which stands for El Niño Southern Oscillation, is the cycle of consistent
and strong changes in sea surface temperature, air pressure and winds
in the tropical Pacific Ocean. The two phases, El Niño and La Niña, typically
take three to five years to complete the cycle.

El Niño is the warm phase of the cycle, when the sea surface temperature in the tropical Pacific is above average. Its opposite, La Niña, is the phase when the temperatures are below
average. The warming and cooling affect the level and patterns of tropical
rainfall, which in turn has an effect on worldwide weather patterns and
hurricane frequency and severity.


El Niño is associated with lower-than-average tropical storm and hurricane
activity in the Northern Atlantic due to higher-than-average vertical
wind shear resulting fromthewind patterns during this phase of ENSO. The
probability of hurricanes and hurricane landfalls in the Caribbean and other
parts of the North Atlantic is significantly reduced during the regular hurricane
season.

At the same time, the weather patterns lead to an increase in
tropical storms and hurricanes in the eastern tropical North Pacific.Results of
the La Niña phenomenon are the opposite: storm formation and hurricane
activity are increased in the North Atlantic during the hurricane season,while
in the Pacific the probability of hurricanes is lower than average. These two phases of ENSO are not equal in time.

El Niño rarely lasts longer than one year, while La Niña tends to take between one and three years. There is no strict cyclicality here, in the sense that each of the two phases can have shorter or much longer durations than expected. The general relationship, however,
usually holds, with periods of increased hurricane activity in the Atlantic
being longer than periods of decreased activity.

Technically speaking, El Niño and La Niña are not truly two phases of the
ENSO cycle. The end of El Niño leads to an ENSO-neutral period, which
may not be followed by a pronounced La Niña phenomenon and can
instead go back to the El Niño stage. Similarly, La Niña may not be followed
by a pronounced El Niño stage.

ENSO affects not only the frequency but also the severity of hurricanes.
One reason for this is the vertical wind shear effect, where hurricane intensity in the Atlantic is dampened during El Niño and increased during La
Niña. In addition, the tropical storm formation centres differ slightly and the
hurricanes follow different tracks. La Niña results not only in a greater
frequency of hurricanes in the Atlantic but also in a greater probability of
hurricanes being formed off the west coast of Africa. These hurricanes have
a higher chance of increasing in intensity and making a landfall in the US or
Caribbean as major hurricanes.

The following figure shows an anomalous increase in sea surface temperature
indicative of the arrival of El Niño and the expectation of lower hurricane
activity in the Atlantic.

2 Medium term

AMO, which stands for Atlantic Multidecadal Oscillation, is a cycle of
consistent and strong changes in sea surface temperature in the North
Atlantic. The cycle is believed to be on the order of 70 years, with the up and
down phases approximately equal in time. The amplitude of the temperature
variations due to the AMO is much milder than that resulting from
ENSO, and the changes much slower. It is believed that we are currently in of the warm phase. This phase is expected to end between 2015 and 2040.

AMO has some effect on the overall frequency of tropical storms and
hurricanes, with warmer temperatures contributing to the tropical storm
system development and colder temperatures leading to a reduction in tropical
storms.

This correlation is not strong and the effect is usually
disregarded. However, during the warm phases of the cycle there is a
greater chance of major hurricanes compared with the average; the chance
is lower during the cold phases. This effect is unambiguous and the correlation
is strong.

3 Medium to long term

Climate change, in particular the increase in seawater temperature, has a
strong potential to increase both the frequency and the severity of the hurricanes
landfalling on the Atlantic coast of the US. Some of the change is the
result of human activities.

Global warming, recognised by the majority of
the scientific community, is part of the overall climate change. There is no
consensus on the exact manifestations of and the speed at which climate
change is happening. Some would argue that categorising climate change as
having medium- to long-term effect is wrong, and that substantial changes
are already happening rapidly and will accelerate.

The risk of abrupt climate change triggered by concurrent development of several factors has been repeatedly pointed out. Even those who subscribe to the global-warming
view without any reservations are unclear on the long-term effects of this
process. In fact, some research has suggested that the increase in the
seawater temperature will lead to a significant increase in hurricane activity
in the North Atlantic, but that at some point the process will reverse itself
and the hurricane frequency will actually decrease even if the temperature
continues to rise. This, however, is a minority opinion.

While global warming remains a controversial topic, in particular because
different people seem to attribute different meanings to the term, it is widely
accepted that seawater temperature has been rising and that the probability
of hurricanes in the North Atlantic is increasing as a consequence. This
correlation has direct applications for hurricane modelling.

INVESTOR VIEWS ON MACRO-SCALE FREQUENCY AND SEVERITY EFFECTS

In the analysis of catastrophe insurance-linked securities tied to the risk of
hurricanes, investors have a short-term view due to the relatively short tenor
of these securities. Whether the probability of hurricanes will be greater in
15 years is not germane to the probabilistic analysis of cashflows from a catastrophe bond that matures in two years. To the degree that long-term phenomena such as climate change are already affecting the probability of hurricanes, they are relevant to and should be incorporated in the analysis.

The difficulty is in having to work with very limited data samples, because,
sometimes, these can provide only anecdotal evidence of the degree to
which long-term processes are already affecting hurricane development and
will continue to do so within the period an insurance-linked security is
expected to remain outstanding.

In practice, it is currently very difficult to
separate and then separately model effects of the general climate change.
Shorter-term effects such as ENSO, on the other hand, can be better
modelled and incorporated in the analysis. To a lesser degree, the same is
true in regard to AMO. Other processes, such as the overall warming related
to climate change, are often incorporated indirectly through their influence
on the observed parameters of the better-understood processes of storm
formation and development.

There is a broad issue of whether, and to what degree, catastrophe models
should reflect the observed increase in hurricane activity in the North
Atlantic. Following Katrina and the 2004–2005 hurricane seasons in general,
there was an almost universal conviction that the frequency of hurricanes in
the widely used commercial models was significantly understated.

(There were also concerns about how other modules of the models performed, and
whether the damage and loss severity were understated.) Since then, the
models have been modified to produce loss results that are greater than
would be expected based purely on long-term historical data, either as the
main output or as an option available to the user.

The change reflects the view that the long-term observations do not represent the current atmospheric conditions that affect formation, development and landfalling of
tropical storms and hurricanes. This important practical issue is discussed
further below and in other articles.

Incorporating short-term effects such as ENSO in both the models and the
general analytical approach can better capture the risk profile of insurancelinked
securities and provide competitive advantage to investors able to do
it. For example, if El Niño starts, which can happen fast and unexpectedly,
short-term probabilities of North Atlantic hurricane losses will immediately
be affected. This affects the risk profile of the insurance-linked securities
exposed to this risk.

The knowledge of lower expected hurricane activity has
immediate application in pricing new insurance-linked securities and those
that can be traded in the secondary markets. Another practical application is
reassessing portfolio risk and return profile in light of the information on El Niño’s start. This reassessment might identify a change in the risk and
return profile of the overall ILS portfolio. The practical result would be a
conclusion regarding which risk buckets have to be filled and which
reduced, and the right prices for doing so.

Knowledge of expected changes in hurricane activity in the short term,
along with the ability to quantify the degree of the change, can create a
competitive advantage in the environment when many investors are not
using proper models at all and few are able to incorporate new information
in their modelling process.

With some exceptions, quantifying the impact of
new information such as the start of El Niño is not performed by the modelling
firms. Users of the models might have a view on the adjustments to
parameters that have to be made, but are unlikely to be able to properly
incorporate these changes in the standard modelling tools. This area is ripe
for improvement; new approaches are expected to be developed in the near
future. For now, some use adjustments made primarily on judgement. These
adjustments might or might not be implemented at the assumptions level,
as opposed to modifying the results of modelling.

The ability to reflect short-term frequency and severity effects of atmospheric
processes to properly assess risk is an advantage in trading
catastrophe bonds; it is an even greater advantage in investing in and
trading shorter-term instruments such as ILWs and catastrophe derivatives.
There is also a question of making better predictions of landfall probabilities
and associated losses of tropical storms that have already formed, which is
important in “live cat” trading; but these very short-term predictions have a
low degree of dependence on the macro-scale hurricane frequency effects
described here.

The discussion about reflecting macro-scale frequency effects in quantifying
the natural catastrophe risk in insurance-linked securities is irrelevant
to most investors, since they do not attempt to make any adjustments. Their
analysis might still capture some of these effects to the degree that the standard
modelling software packages used in catastrophe modelling might
give greater weight to recent years, as opposed to being calibrated based
simply on the long-term historical record of observations.

While this approach on the part of investors is inadequate and easy to criticise, it
reflects the degree of difficulty of determining and quantifying the effects of
macro-scale atmospheric processes on hurricane activity. A high level of
expertise is required to do it properly, and there is a significant degree of
uncertainty associated with these adjustments.

EVOLUTION OF INVESTOR VIEWS ON CATASTROPHE MODELLING

Incorporating short-term effects in catastrophe modelling has grown in
importance over time. Given that, for catastrophe bonds, buy-and-hold used
to be the only investment strategy, modelling was often performed only
once. Investors rarely tried to perform any real modelling and relied fully on
the analytical data in the offering circulars.

Many did not do even that and
based their investment decisions on other considerations, of which bond
ratings were the most important. Of course, even then there were investors
with deep understanding of insurance-linked securities; however, they
tended to be an exception rather than the rule. Even investors with a high
level of expertise in catastrophe risk, such as reinsurance companies, often
based the decisions on only a rudimentary overview of the summary
analysis provided in the offering circulars.

Some attempts to revisit the original
analysis would sometimes take place in the context of portfolio
construction, with a single focus on avoiding excessive risk accumulation in
some combinations of geographies and perils. Again, this statement is not
universally applicable, since from the very beginning some of the players in
the ILS market have been very sophisticated.

As the market has continued to develop, the level of sophistication of
many investors has grown with it, even though a significant disparity
remains. There are some ILS investors who lack any analytical expertise, and
some who believe they understand the analytics while in reality they do not.
In general, however, the current landscape is very different from what it
was in the beginning of the cat bond market. There are more new issues and
bonds outstanding. There is a sizable and growing secondary market for
catastrophe bonds.

This creates new opportunities for portfolio rebalancing
and optimisation. In addition, the ILW market has grown significantly.
Catastrophe derivative markets have reappeared and are growing as well.
Investors able and willing to take part in these markets and not be confined
to investing in catastrophe bonds have new options to generate higher riskadjusted
return by investing in catastrophe risk insurance-linked securities.
Direct hedging can be done in managing an ILS portfolio. The markets
remain inefficient and liquidity insufficient, but the array of options available
to investors has certainly expanded.

The ability to better model the risk has always been important in the
analysis of individual securities. The better tools now available for this
modelling have given investors a greater degree of confidence in the
analysis and opened new options not available several years ago.

RELATIONSHIP BETWEEN ILS INVESTOR SOPHISTICATION AND THE LEVEL OF ILS ANALYTICAL EXPERTISE

There is an obvious connection between the level of investor sophistication
and the ability to analyse the securities being invested. However, investing
in insurance-linked securities without being able to fully analyse them does
not necessarily put an investor in the “naïve” category.

There could be very good reasons for arriving at a well-thought-out decision not to expand
resources on developing internal expertise in insurance-linked securities,
but instead to allocate a small percentage of the overall funds to this asset
class without performing in-depth analysis.

One of the reasons could be the diversifier role that insurance-linked securities can play in a portfolio. Given a very small percentage allocation to ILS, for some investors the
cost–benefit analysis might not justify developing an expertise in this asset
class, though they may still have sufficient reasons for investing in ILS.

An even more important development stemming from the advances in modelling catastrophic events is the ability to better model and optimise portfolios of catastrophe insurance-linked securities. The new options available to investors – more new issuances; the development of secondary markets in catastrophe bonds, combined with a greater number of
outstanding bonds; the availability of ILWs and catastrophe derivatives,
both exchange-traded and over-the-counter – have also increased the need
for models that can be used in portfolio and risk management.

The shift from the buy-and-hold investment strategy as the only available option to
the ability, no matter how limited, to optimise and actively manage a portfolio
of insurance-linked securities is a sea change for a sophisticated
investor. Modelling insurance-linked securities on a portfolio basis has
increased the emphasis on modelling.

Some of the new modelling tools developed specifically for investors are described later in this article. A sophisticated investor can also take advantage of the live cat trading
opportunities arising when a hurricane has already formed and is threatening
an area that has significant insurance exposure. Short-term forecasts
can then be combined with broader portfolio modelling to take advantage
of the opportunities to take on risk at attractive prices, or to offload excess
risk in the portfolio.

So far, very little live cat trading has been done, but at least some growth in this area is expected. Improvement in the ability to model catastrophe risk contributes to the
development of the ILS markets. Enhanced tools give investors a higher
degree of confidence and open up new options.

At this point, however, most investors do not utilise the tools already available, and many make their investment decisions based primarily on judgement and a back-of-the-envelope
type of analysis. While there are some extremely sophisticated players
in this market, there is significant room for improvement in investor understanding
and modelling of catastrophe insurance-linked securities.

ELEMENTS OF HURRICANE MODELLING

Doubt is not a pleasant condition, but certainty is absurd.
Voltaire

There is a very high degree of uncertainty associated with hurricane losses.
It surrounds all elements of a hurricane model – from the frequency and
location of storm formation to its tracks and intensity, and the possible landfall
and resulting insured losses. The very high degree of uncertainty has
been a continuing source of frustration for many investors who rely on the
output of black-box-type modelling tools such as the analysis summarised
in offering circulars for cat bonds.

It is even more frustrating for those fewinvestors for whom the modelling tools are not black boxes and who understand the assumptions and the modelling of individual processes within the broader analytical framework. Their superior understanding does not eliminate
the uncertainty and might even increase the perception of the degree
of uncertainty in their minds.

We need to keep in mind that the obvious uncertainty involved is not unique to insurance-linked securities tied to catastrophe risk: to some degree it is present in any security and financial instrument. Insurance-linked securities are unique in the type of risks they
carry; they are not unique in the carrying of risk per se. Every security carries
some degree of risk, uncertainty and unpredictability; assuming the risk is
what investors are paid for. In the case of insurance-linked securities, one of
the ways to reduce the uncertainty is to improve the modelling of hurricanes
and the damage they cause.

There exists a considerable body of research on modelling atmospheric
phenomena such as storms and hurricanes. Catastrophe models used in the
insurance industry and in the analysis of insurance-linked securities are
based on some of this research, as described earlier.

A comprehensive overview of the atmospheric science on which the commercial models are
based would take up a thick volume and cannot be provided here. In most
cases, understanding all of the science is completely unnecessary for an
investor analysing insurance-linked securities. It is important, however, to
have some basic understanding of the science and assumptions used in catastrophe
software packages and avoid treating these tools as black boxes that spit out results based on user input.

Among the many advantages of understanding
the basics of the science and assumptions used by the models is the
ability to better understand the sensitivity of results and the degree of uncertainty
involved. Another important advantage is understanding some of the
differences between the models.

Some elements of the modelling of hurricane risk and related basic scientific
concepts are discussed below. They are not intended to educate a reader
on the hurricane science as such, or even its use in commercial catastrophe
models: rather, the purpose is to provide an illustration of how the models
work, by describing selected issues relevant to the topic.

Modelling hurricane frequency

The number of storms in a hurricane season can be simulated by sampling
from the hurricane frequency distribution. When the frequency of hurricanes
or hurricane landfalls is modelled directly, there are three main
choices for the probability distribution:

• Poisson;
• negative binomial; and
• binomial.

Poisson distribution is the natural first choice as it is for most frequency
distributions. Binomial distribution might be appropriate where the sample
variance is less than the sample mean. This is unlikely to be the case in
events with such a high degree of uncertainty as hurricanes; the fact that
there can be several hurricanes during the same time period further complicates
the use of this distribution.

In fact, the variance generally exceeds the mean, leading to the recent adoption by many of the negative binomial as the distribution of choice for hurricane frequency. Most of the standard catastrophe models utilise the negative binomial distribution for hurricane
frequency in Florida; some allow users the choice between Poisson and
negative binomial distributions.

Despite the recent shift towards the use of the negative binomial distribution,
Poisson distribution is still commonly used as well. When considering
the choice of probability distribution for hurricane frequency, parameterisation
might be a bigger issue than the analytical form of the distribution. This
is particularly challenging because of the varying views on the changes in
hurricane frequencies over time.

In fact, the regime switch view of the hurricanefrequency affects both the choice of the parameters of the distribution and the choice of the distribution itself. It is possible that the statistically significant fact of the sample variance exceeding the sample mean is the
result of inappropriately combining in the same sample unadjusted observations
from time periods that have had different mean hurricane
frequencies due to climate oscillations or other changes.

If this is the case, the choice of Poisson distribution over the negative binomial might be preferable. In this context, the choice of the distribution is dependent on the choice
of the distribution mean: if it is determined based on the full historical database
of observations, with all observations given the same weight, negative
binomial distribution seems to almost always outperform Poisson in backtesting
regardless of the geographical region being considered.

Hurricane frequency and intraseasonal correlation

There is an ongoing debate about whether the occurrence of a hurricane, in
particular a major hurricane, during the hurricane season means that there
is a greater probability of another hurricane occurring in the remainder of
the season. In other words, there is a question of whether the frequency
distribution changes if it is conditioned on an occurrence of a hurricane.

The phenomenon in question is sometimes referred to as hurricane clustering.
The rationale for the view that the probability of hurricanes increases
under these circumstances is that a major hurricane is more likely to develop
if the general atmospheric conditions are more conducive than average to
hurricane formation. This in turn implies a greater-than-otherwise-expected
chance of additional hurricanes during the season.

In the analysis of insurance-linked securities, the issue of intra-seasonal
correlation is of particular importance for second-event bonds and second event
catastrophe derivatives. Of course, it is important in ILS analysis in
general for valuation purposes as well as for evaluating opportunities in the
catastrophe bond secondary markets. It could be of even greater consequence
in the context of investment portfolio management.

If the probability of hurricane losses on the US Atlantic coast has increased, it could affect
several securities and have a magnified effect across the portfolio.
In practice, we would be hard pressed to find investors who go through
the process of calculating conditional probabilities of hurricane events. The
standard commercial catastrophe models do not have an easy way to adjust
the probabilities in the middle of a hurricane season based on the occurrence
of an event such as Category 3 hurricane making a landfall in the US or the
Caribbean. There have been attempts to take the intra-seasonal auto correlation
into account in modelling second-event catastrophe bonds.

A better approach than auto correlation models or making adjustments to the frequency distribution based largely on judgement would be to instead
adjust the atmospheric parameters in the model. If the occurrence of a hurricane
was indicative of changing atmospheric conditions, then the best way
to reflect it in the model is by making changes to these assumptions. The
approaches of using auto correlation methods or of making adjustments
based primarily on judgement are also important.

Wind field modelling

Storm track modelling and modelling of the characteristics of the storm are
an essential part of the overall hurricane modelling. Characteristics of the
storm at a particular location include central pressure, direction, forward
velocity, maximum winds, air pressure profile and many others.
Some elements of wind field modelling are shown in the following diagram. The
approach shown is just one of many ways to build wind field models.

The important output of wind field models that is used in insurance catastrophe-
modelling software packages is the wind characteristics after
hurricane landfall, at specific locations where insured exposure is located.
Parameterisation of the models is a challenging task that has the potential
to introduce uncertainty and, in some cases, lead to significant errors.

While historical observations are used to calibrate and validate the models, the
sample of observed events is not big enough to credibly estimate a large
number of parameters. A very complex and scientifically sound theoretical
wind field model might be completely useless in practice if it requires estimating
a large number of parameters based on empirical data. This
statement is not limited to wind field models and is applicable to most
elements of hurricane modelling.

Probability distributions of some wind field parameters

In the same way as there are several wind field models, there is more than
one way to model individual parameters used in these wind field models.
Most wind field models use the same general parameters.

Below we look at the examples of probability distributions of some of the stochastic parameters, in particular the ones used in the standard commercial catastrophe
models, as these are of most interest to the practitioner.

Annual frequency

Generating storm formation frequency technically is not part of wind field
modelling and comes before it, as does generating hurricane landfall
frequency in most models. Hurricane frequency has been covered above,

Wind field modelling is a critical part of simulating hurricanes and resulting
insurance losses. Various models have been developed; even for the same
model, parameterisation differs from one modeller to another. For illustrative
purposes, below we show selected elements of one of the wind field
models.

Pressure isobars of a cyclone can be modelled as concentric circles
around its centre. One of the standard models for the radial distribution of
surface pressure is

 

where p(R) is the pressure at a distance R from the centre of the cyclone, p0
is central pressure, Rmax is radius to maximum winds, Dp is the central pressure
difference, and B is a scaling parameter reflective of pressure profile.
There are a number of models for the Holland parameter B, one of the
simplest being B = a + bDp + cRmax , where a, b and c are constant. 

In this formulation, dependence on latitude is taken into account indirectly
through other parameters. A popular wind field simulation model is based
on the gradient balance equation of the following form:

Vg is the gradient wind speed at distance R from the centre and angle a
from the cyclone translational direction to the site (clockwise considered
positive), r is the air density, f is the Coriolis parameter and VT is the
cyclone translational speed.
Using the pressure distribution model described above, we obtain the
following formula for gradient wind speed:

Gradient wind speed Vg can then be used to determine wind speed at
various heights. A number of decay models can be used to simulate the
evolution of wind parameters upon landfall. These will be utilised in calculating
wind gusts over land, taking into account surface roughness and
general topography.

where two functional distribution forms – Poisson and negative binomial –
have been described as the most appropriate, with a general shift to using
the negative binomial distribution because the variance of observed hurricane
frequencies typically exceeds its mean. Parameters of the distribution,
whether negative binomial or Poisson, are estimated based on a smoothing
technique to account for the low number or lack of observations in most
locations.

Landfall locations

If the landfall frequency is estimated directly by location based on one of the
methods described above, there is no need to use any distribution to estimate
landfall location probabilities. Otherwise, given the general hurricane
landfall frequency, the probability of landfall by specific location can be
distributed based on smoothing of empirical data or using a physical model.
Other approaches can be used as well.

Central pressure

Smoothed empirical distributions can be used for central pressure at and
following landfall. The same approach is possible but harder to implement
for modelling hurricane central pressure before landfall. While central pressure
does not easily lend itself to being described by any standard functional
probability distribution, the use of Weibull distribution has produced
acceptable fit. Strong hurricanes are much rarer than the weak ones, and the
Weibull distribution, with properly chosen parameters, captures this relatively
well.

Forward speed

Smoothed empirical distribution specific to a landfall gate is one of the
choices for modelling hurricane forward speed. Similar to the central pressure
distribution, that of forward speed is skewed, with very fast forward
speeds being much less common than slower speeds. However, based on
historical observations, the degree of skewness is generally lower.
Lognormal distribution is a good choice for modelling storm forward speed
in most situations.

Radius to maximum winds

Lognormal distribution can be used for modelling Rmax, with its parameters
depending on central pressure and location latitude. The lognormal distribution
needs to be truncated to avoid generating unrealistic values of Rmax.

Gamma distribution has also been used for stochastically generating radius
to maximum winds, producing acceptable results when limited to modelling
the Rmax variable at landfall as opposed to including its modelling over
open water. Another way to generate Rmax values is by using one of the
models where logarithm of Rmax is a linear function of central pressure
(and/or its square) and location latitude. 

Coefficients in the linear relationships are determined based on empirical data. Then Rmax is not simulated directly, but rather is calculated as a function of latitude and the simulated
value of central pressure. Other models can also be used.
These are just some of the random variables simulated in catastrophe
models. Many others need to be modelled, including such important ones as
wind dissipation overland, in order to ultimately derive hurricane physical
parameters after a landfall.

DAMAGE MODELLING
In catastrophe models, the next step after simulating physical effects of a
hurricane (such as peak gusts and flood depth at specific locations) is determining
the damage they cause. Conceptually, this process is very
straightforward. It involves the following basic steps:
1. For each individual location in the insured exposure database,
consider

• simulated physical characteristics of the storm that are relevant to estimating potential damage;
• characteristics of the insured property at the location.

2. Identify the damage functions corresponding to the hurricane’s physical
parameters (peak gusts) and the vulnerability classes of insured
buildings and contents at the location.
3. Apply the damage functions to the replacement value of the insured
property to calculate the loss.
Detailed information on the insured property is essential for assessing its
vulnerability to hurricanes. The information should include the following,
in as great detail as possible:

•  precise location of the insured property (street address, ZIP code, CRESTA, etc.);
• vulnerability characteristics (construction type, height and footprint size, year of construction, occupancy type, mitigating factors, etc.); and
•  replacement property value.

Vulnerability functions are based on historical data and structural engineering
analysis. Their details represent a highly proprietary component of
commercial catastrophe models that can be a significant differentiator
among the models. The exact definition of a vulnerability function is the
relationship between the mean damage ratios and the peak gusts, where the
mean damage ratio relates the expense of repairing the damaged property
to the replacement cost of the property.

Modifications to vulnerability functions or subsets of vulnerability functions
can be based on secondary characteristics or mitigation measures such
as roof type, roof strength, roof-to-wall strength, wall-to-floor and wall-tofoundation
strength, opening protection and others. The variables are
largely the same for all models since they are a function of the type of exposure
information collected by insurance companies.

The way vulnerability functions are determined and modified differs, sometimes significantly,
from one model to another. Some models use additional variables such as
wind duration to better estimate damage to insured property from hurricanes.
The fact that damage modelling follows very simple and logical steps
does not imply the ease of building a module for its calculation as part of a
catastrophe model.

The effort going into determining and refining vulnerability
functions cannot be overestimated. Complex structural engineering
studies have been conducted for this purpose and a large amount of historical
hurricane damage data has been analysed. This is a continuing process
as more precise site information becomes available, building codes change
and other developments take place.

FINANCIAL LOSS MODELLING

Once the damage for each insured location has been calculated, it can then
be translated into the amount of insured loss by applying to it policy terms
and conditions including its deductible and limit. Loss triggers, insurance
coverage sublimits and other factors are also taken into account in the calculations;
for reinsurance purposes, other factors such as attachment point are
also part of the loss calculations.

This process too is very straightforward in
its implementation as long as all the necessary data inputs are reliable.
Adjustments to the process, when such are required, can introduce a
degree of complexity. Adjustments include taking into account demand
surge following a catastrophic event.

WIND AND EARTHQUAKE STRUCTURAL ENGINEERING ANALYSIS

The ability to estimate potential damage to insured structures depending on
the physical characteristics of a hurricane or an earthquake is a challenging
structural engineering task. Two separate disciplines, hurricane engineering
and earthquake engineering, have developed to deal with engineering
aspects of hurricane and earthquake hazards.

While the broader focus of the disciplines is on designing, constructing and maintaining buildings and infrastructure to withstand the effects of catastrophic events, in insurance
catastrophe modelling the emphasis is on quantifying the damage that
would result from hurricanes and earthquakes of various intensities. Similar
principles can also be applied to the risk of manmade catastrophic events
such as acts of terrorism.

Estimating the dependence of mean damage ratios on hurricane peak
gusts or earthquake physical characteristics for various types of structures is
the process of constructing vulnerability functions, which are an essential
part of the damage calculator in insurance catastrophe models.
Constructing sets of vulnerability functions for specific geographical areas
is necessary to take into account the overall topography, building codes
and the history of their change over time, and other factors.

Demand surge

A catastrophic event such as a hurricane landfall or an earthquake can result
in the increase of costs of repairing the damage and other expenses covered
by insurance policies above the level of claim costs expected under normal
circumstances. This effect is referred to as demand surge, reflective of the
increase in costs being driven by a sharp increase in demand while the
supply lags behind.

An example is the shortage of building materials following a major hurricane, when many properties are damaged and all of them require building materials for restoration, all at the same time immediately following the hurricane. The cost of building materials naturally
goes up to reflect the demand–supply imbalance created by catastrophic
events.

The post-event shortage expands to the labour costs, which also
affect the cost of rebuilding the damaged property. Additional living
expenses can also grow after a large catastrophic event, further contributing
to losses suffered by insurance companies.

To account for demand surge, insurance catastrophe models can apply
special demand surge or loss amplification factors to insurance losses. The greater the magnitude of a catastrophic event, the greater the demand surge
effect. The effect applies to different parts of insurance coverage to different
degrees; consequently, demand surge factors differ as well. Sometimes the
factors are further refined to reflect the various degrees of the demand surge
effect, for example on the cost of rebuilding various types of property.

Aggregate approach

An aggregate approach, as opposed to the more detailed location-by-location
modelling, starts before the financial loss module, in the analysis of
hurricane damage. The goal here is to arrive at aggregate insured losses for
an individual risk portfolio or even for the whole insurance industry. In this
approach, portfolio-level information is used in the calculations to arrive at
the loss distribution, as opposed to analysing each individual risk independently
and then aggregating the losses across the portfolio.

Inventory databases of property exposure are utilised to help accomplish this goal,
with the data aggregated by location (such as ZIP or postal code) and
including information on the types of property, vulnerability degrees, type
of coverage, etc. The calculations consider aggregate exposure data by location,
estimate the average damage and then translate it into financial losses.

When this is done not for an individual portfolio of a specific insurance
company but for the whole insurance industry, the result is a figure for
industry-wide losses by geographic area (for example, all of Florida), the
probability distribution of which is important for larger primary insurance
writers, and even more important for reinsurance companies.

There are other ways to calculate aggregate losses, which are based on
more granular analysis and the use of databases of insurance policies from
several insurance companies, and then extrapolating the losses to the total
insurance industry based on insurance premiums or another measure of
exposure. Some modelling companies might have developed such databases
by combining data from the companies that provided them with this
information.

In the context of insurance-linked securities, aggregate losses suffered
by the insurance industry are important in catastrophe bonds with an
industry loss trigger, in industry loss warranties (ILWs) and in catastrophe
derivatives.

 

Read More»